动态规划——何为动态规划

本系列将对动态规划进行讲解，分为上中下三部曲。本篇将来详细说说什么叫做动态规划和标准解题步骤

何为动态规划

我们给出百度百科的解答：

此处有几个重要的要素：

最优子结构
简称：DP

下面我们依次讲解

最优子结构

动态规划的灵魂就是 将一个复杂结构转换为多个子结构，并找到最优的子结构，过程如下：

定义“状态”
找到“状态转移方程”

动态规划，顾名思义，它是一个 动 的过程，我们需要不断规划它的每一个状态

所以我们应该先找到子结构的的初始状态，再去找到状态更改的状态转移方程

这时就需要利用一个表，来存取每个子结构的状态，即Dp表

Demo

以 LeetCode 第5题 最长回文子串为例：

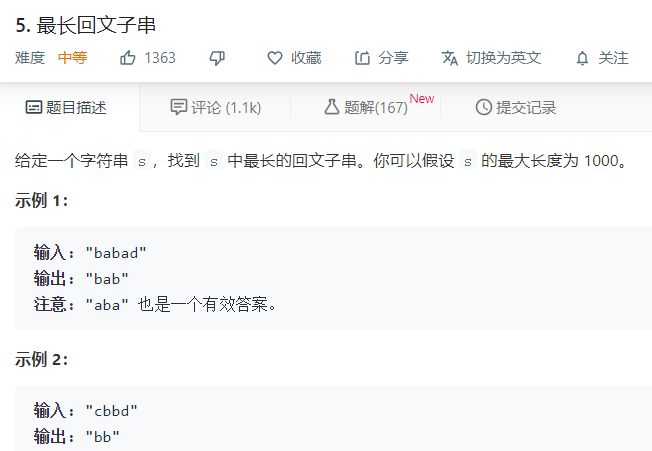
这道题，最容易想到是暴力递归，每一个组合都试一下，此处略去

其次是巧妙地中心扩散：

以 “babad” 为例，当索引 i 到了第三个字符的 b 时，以b为中心进行左右同时扩散
然后比较 i-1 i+1 这两个字符
- 相等则说明 arr(i-1, i+1) （表示索引i到j的字串）范围内的串为回文，并继续向下比较；
- 若不等，则说明不是回文，索引 i 向下继续比较

我们要使用的动态规划原理和中心扩散类似，不过是中心扩散原理的逆过程：

若想知道 string(i, j) 是否为回文，那么我们需要知道 string(i+1, j-1) 是否为回文，依次比较
那么，状态我们就得出来了，arr[i ,j] 的意义为，字串索引 i 到 j 是否为回文，用bool类型表示，0代表不是，1 为是
所以，我们就可以得到一个表，即一个二维数组，我们把它叫做 dp表
状态我们已得出，那么状态转移呢？
我们知道了 dp[i, j] 的状态由 dp[ i+1, j-1] 决定，所以，可以理解为 dp[i+1, j-1] 转移到 dp[i, j]
那么，确定 arr[i, j] 是回文只需要 dp[i+1, j-1] == 1一个条件么？
- 答案显然是否定的，我们还需要 i 所在的字符等于 j 所在的字符，这样才能继续向下推进
- i+1,j-1总会有一个界限的
  
  1、当原字符串的元素个数为 3 个的时候，如果左右边界相等，那么去掉它们以后，只剩下 1 个字符，它一定是回文串，故原字符串也一定是回文串；
  
  2、当原字符串的元素个数为 2 个的时候，如果左右边界相等，那么去掉它们以后，只剩下 0 个字符，显然原字符串也一定是回文串。
  
  把上面两点归纳一下，只要 s[l + 1, r - 1] 至少包含两个元素，就有必要继续做判断，否则直接根据左右边界是否相等就能得到原字符串的回文性。而“s[l + 1, r - 1] 至少包含两个元素”等价于 l + 1 < r - 1，整理得 l - r < -2，或者 r - l > 2。
综上所述，动态转移方程为：dp[l, r] = (string[l] == string[r] and (r - l <= 2 or dp[l + 1, r - 1]))

代码实现（Java版本）

public class Demo {
    public static void main(String[] args) {
        //动态规划版本
        String string = "ac";

        String big = palind(string);

        System.out.println(big);

    }

    private static String palind(String string) {

        int length = string.length();

        //判断字符串是否为空
        if (length == 0)
            return "";

        //长度为 1去，返回本身
        if (length == 1)
            return string;

        // 最大回文串（默认为 字符串的第一个，防止只有一个字符的情况）
        String maxString = string.substring(0,1);

        //dp表  默认为 0
        int[][] dp = new int[length][length];

        //因为 dp表中每个元素需要依托于左下角元素，所以，我们应从 right 循环，内循环是 left
        for (int right = 1; right < length; right++) {
            //使 left<right ，可避免元素 left 和 right 指针重合的情况
            for (int left = 0; left < right; left++) {
                /**
                 * 检验 left 和 right 对应 char 是否相等
                 * 相等时 left和right有两种，一种是 right-left <= 1 即此时 right 和left 紧邻或				  者 right==left（不考虑此情况）
                 * 当不上上述情况时，那么就要 满足
                 */
                if (string.charAt(left) == string.charAt(right) && ( (right-left <= 2) || dp[left+1][right-1] == 1 )) {
                    System.out.println("left=" + left + ", right=" + right);
                    dp[left][right] = 1;

                    if ( right - left >= maxString.length()-1)
                        maxString = string.substring( left, right+1);
                }
            }
        }
        return maxString;
    }
}

参考地址

动态规划入门三部曲（上）

何为动态规划

最优子结构

Demo

代码实现（Java版本）

CATALOG