算法时空 算法

算法时空第21讲 线性时间的排序

次序统计量

Posted by Twany on July 31, 2019

最大元和最小元

求数组arr的最大元和最小元

如果用普通方法来解的话，是要先创建哨兵，然后依次与哨兵比较，冒泡法得出。

最大值和最小值均如此，复杂度为o(2n-2)

更为简易的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

if(arr.length() % 2 == 0){  //当 n 为偶数
    int min = arr[0];
    int max = arr[1];
}else{  //为奇数
    int min = arr[0];
    int max = arr[0];
}

if( x<y ){  //一次取出两个元素，当 x 比较小的时候
    min = x<min ? x : min;
    max = y<max ? max : y;
}else{  //y 比较小
    min = y<min ? y : min;
    max = y<max ? max : y;
}

上述代码，我们进行了n/2组的比较，每组比较比较了3次，所以复杂度为 o(3*n/2)

期望线性时间的选择算法

问题：存在数组arr，求数组中第K小的元素

思路

我们利用快速排序的方法

  • 在第一次排序中，选择好划分点n 如图，n 为划分点，我们已知n左侧x个元素均小于等于n，右侧大于n
  • 那么，我们可知，n是第x+1最小的元素
  • 将n+1和K进行比较
    • n+1 == K，则n+1就是要找的元素。
    • n+1 < K，说明第K小元素在右侧，继续递归右侧序列
    • n+1 > K，说明第K小元素在左侧，继续递归左侧序列

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

import java.util.Arrays;

import static java.util.Arrays.*;

public class Test {
    public static void  main(String[] args) {
        int[] arr = {4,9,5,11,6,32,49,21,7,8,6,9,2};    //[2, 4, 5, 6, 6, 7, 8, 9, 9, 11, 21, 32, 49]
        int end = search(arr,6);
        System.out.println(arr[end]);   // 7

    }

    //划分方法
    private static int partition(int[] arr, int leftIndex, int rightIndex) {
        int pivot = arr[leftIndex];

        while (leftIndex < rightIndex){
            while (leftIndex<rightIndex && arr[rightIndex] > pivot)
                rightIndex--;
            arr[leftIndex] = arr[rightIndex];

            while (leftIndex<rightIndex && arr[leftIndex] <= pivot)
                leftIndex++;
            arr[rightIndex] = arr[leftIndex];
        }
        arr[leftIndex] = pivot;

        return leftIndex;
    }

    private static int search(int[] arr,int k){
        int left = 0;
        int right = arr.length-1;

        int index = partition(arr,left,right);

        while( index+1 != k){
            if(index+1 < k) //位于右侧
                left = index+1;
            else    //位于左侧
                right = index-1;
            index = partition(arr, left, right);
        }
        return index;
    }
}
注意:
  • 我们此处用到的partition方法和快速排序章节的partition方法实现略有不同，此处是通过覆盖不符合条件的元素，而不是交换。
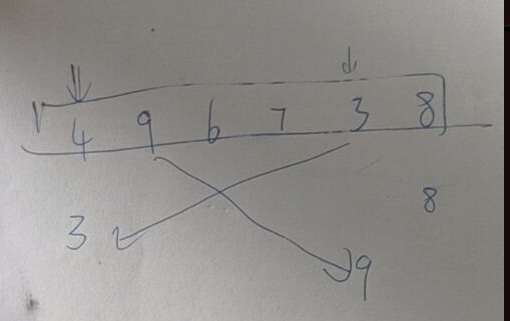
    • 示意图：
  • 我们并不用给数组 arr 完全排序，只需要让其满足枢纽元左右侧大小关系即可。

参考链接：快速找出数组中前k小的元素

笔记

CATALOG