归并排序采用了分而治之的策略和迭代的方法,何为分而治之?
- 分:将原问题分成若干小问题
- 治:分别处理小问题
- 合:以小问题的解构建原问题的解
难在两处:
- 如何巧妙地“分”?
- 如何巧妙地“合”?
下图为归并排序思路:
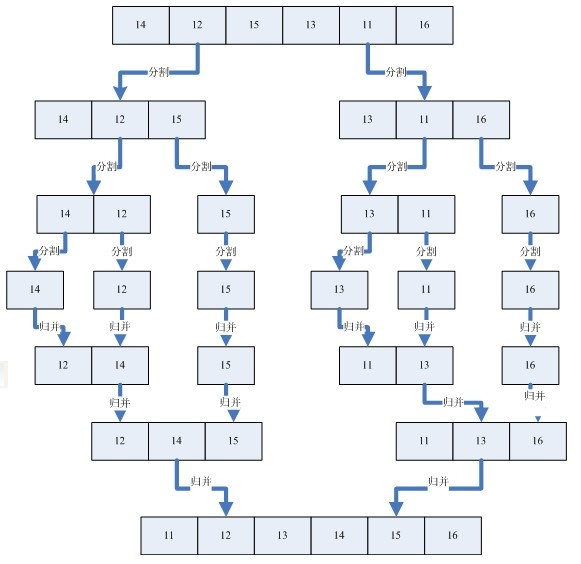
先分再合
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
public class Merge
{
//归并排序
public static void main(String[] args) {
//需要排序的数组
int[] arr = {9,5,3,7,4,9,3,5,1};
//第一次归并(第一个参数为排序数组;第二个为排序左索引,第二个为右索引)
merge_sort(arr, 0, arr.length-1);
//输出排序好的数组
for (int i : arr) {
System.out.println("排序之后" + i);
}
}
//拆分过程
private static void merge_sort(int[] arr, int left, int right) {
//求出要拆分的数组arr中点索引
//int mid = (left+right)/2;
int mid = left + (right-left)/2; //化简其实等于上处的式子,但这样做避免栈溢出
//如果数组中只有一个元素,返回
if(right == mid){
return;
}else{
//左边数组排序
merge_sort(arr, left, mid);
//右边数组排序
merge_sort(arr, mid+1, right);
//两边数组合并
merge(arr, left, mid, right);
}
}
private static void merge(int[] arr, int left, int mid, int right){
/*
* 要合并的是两个数组,给两个数组指针索引,改变则索引加一
* @i 左边数组索引
* @j 右边数组索引
*/
int i=left;
int j=mid+1;
//复刻一个新的数组,新数组只复刻要排序的数组部分(注意长度)
int[] auk = new int[right-left+1];
//数组赋值,先把较小的数移到新数组
while(i <= mid && j <= right){
if(arr[i] < arr[j]){
auk[m++] = arr[i++];
}else{
auk[m++] = arr[j++];
}
}
//如果只有一个数组排序完,另一个还未完
//把左边数组中剩余的数移入数组
while(i <= mid){
auk[m++] = arr[i++];
}
//右边同理
while(j <= mid){
auk[m++] = arr[j++];
}
//新数组覆盖原数组
for (int k = 0; k < right-left+1; k++) {
arr[left + k] = auk[k];
}
}
}
难点:
- 首先要理解merge_sort(),此方法作用是递归调用:使数组变为长度为1。之后再调用合并
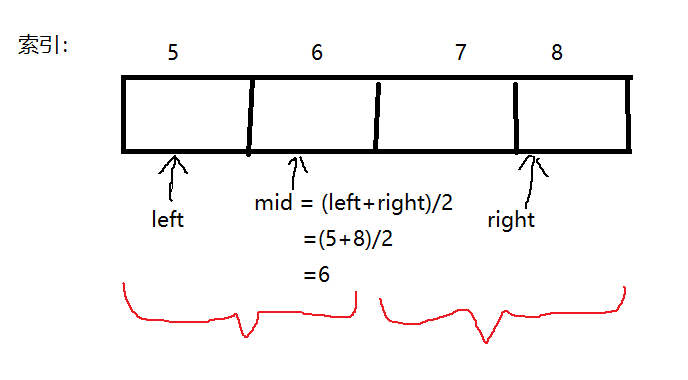
- merge()方法的左右边界取值,注意是否加一减一,因为数组是从0开始,以及mid的取值
cookie
- 防止栈溢出:
int mid = left + (right-left)/2;。让我写肯定是mid = (left+right)/2,但如果最大长度为right位,就尴尬了 - 代码简洁之道:
1 2 3 4 5 6 7
while(i <= mid && j <= right){ if(arr[i] < arr[j]){ auk[m++] = arr[i++]; }else{ auk[m++] = arr[j++]; } }
很简洁的代码,非常值得学习!
参考链接:Java实现归并排序